1.机器学习的基本概念
1.1 什么是机器学习?
机器学习是人工智能的一个子集,其本质就是要设计一种能够提取出数据之间规律的算法。机器学习又分为有监督学习、无监督学习、半监督学习:
- 1.有监督学习:用于分析的数据已经提前进行了分类,打好了标签
- 2.无监督学习:用于分析的数据并未提前分类
- 3.半监督学习:部分数据进行了分类,打好了标签
目前机器学习领域已经发展出了很多有用的方法,例如:支持向量机,回归,决策树,随机森林,强化方法,集成学习,深度学习等等。这些方法可以在一定程度上可以帮助我们对数据进行分类、进行决策。
机器学习的主要功能就是以下两点: - 分类 - 回归
1.2 什么是神经网络?
所谓的神经网络最初就是参考人体神经细胞的结构设计的一种算法结构:
神经网络的结构主要可以分为:
- 输入层:输入层主要负责读取被分析的数据
- 隐藏层:隐藏曾主要负责提取分析数据之间的规律,对信息进行传递和加工
- 输出层:输出层主要是计算机对整个输入信息的分析结果输出
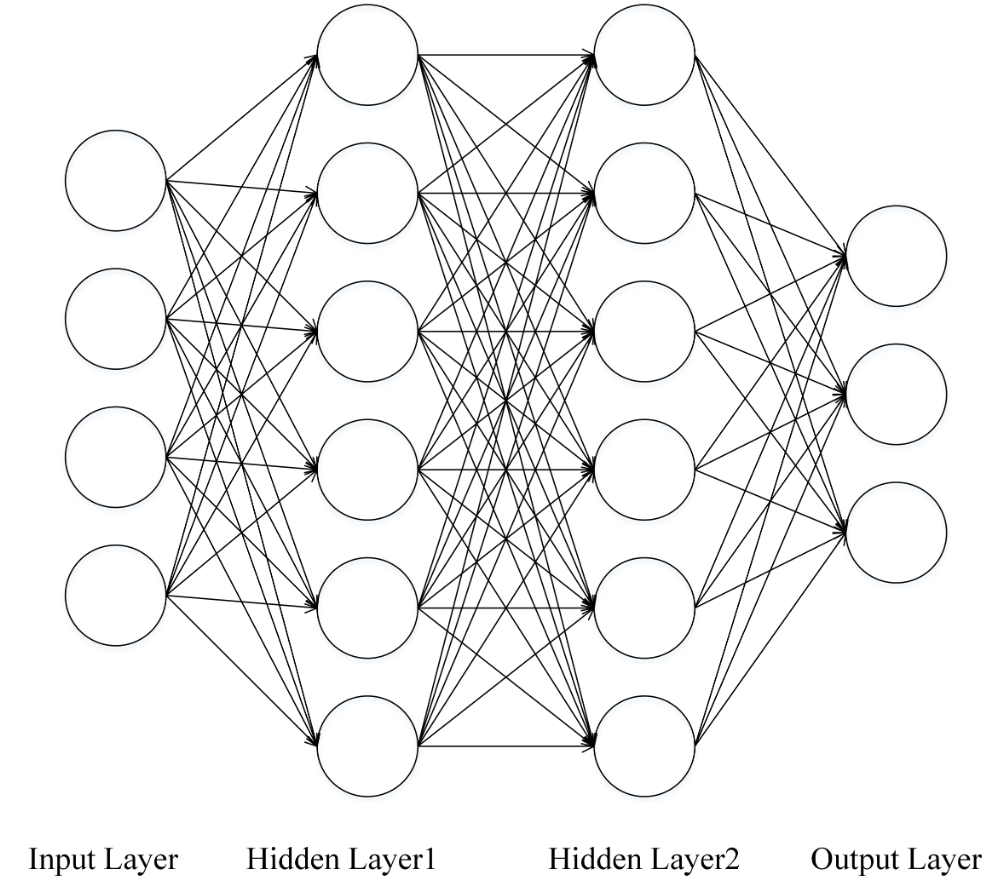
下图所示的神经网络是最为常用的一种全连接(Full Connected, FC)神经网络,它的主要特征为 - 同一层的神经元之间没有连接 - 第 N 层的每个神经元和第 N-1 层的所有神经元相连,第 N-1 层神经元的输出就是第 N 层神经元的输入 - 每个连接都有一个权重
1.3 监督学习的一般步骤
- 1.数据集的创建和分类:数据分成训练集和测试集、标记训练集
- 2.数据增强:对数据增加扰动
- 3.特征工程:特征提取和特征选择
- 4.构建预测模型和损失
- 5.训练
- 6.验证和模型选择
- 7.测试及应用
2.常用python编程库
2.1 Numpy(数学计算库)
Numpy是 Python 语言的一个扩展程序库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。这个库的使用能够为后面的算法实现提供巨大的帮助,尤其是进行矩阵的运算时。安装直接pip安装就可以了。
2.1.1 Numpy Ndarray对象
2.1.1.1 创建Ndarray对象
Ndarray对象是一系列同类型数据的集合,是用于存放同一类型元素的多维数组。常用的创建一个Ndarray对象方式如下:
#使用现有列表创建 import numpy as np a = np.array([[1,2,3],[4,5,6]],dtype=float) print(a)
[[1. 2. 3.] [4. 5. 6.]]
#创建一个初始值为0的数组:numpy.zeros(shape, dtype = float, order = 'C') order='C' 用于 C 的行数组,或者 'F' 用于 FORTRAN 的列数组 np.zeros((2,3),dtype=float64)
array([[0., 0., 0.], [0., 0., 0.]])
# 创建一个初始值为1的数组:numpy.ones(shape, dtype = None(默认float64), order = 'C') np.ones((2,3),dtype=float32)
array([[1., 1., 1.], [1., 1., 1.]], dtype=float32)
在 NumPy中,每一个线性的数组称为是一个轴(axis)。很多时候可以声明axis。axis=0,表示沿着第0轴进行操作,即对每一列进行操作;axis=1,表示沿着第1轴进行操作,即对每一行进行操作。
2.1.1.2 Ndarray对象属性
ndarray对象中有如下较为常用的属性:
| 属性 | 说明 |
|---|---|
| ndarray.ndim | 维度的数量 |
| ndarray.shape | 数组的维度,返回n,m,即n行m列 |
| ndarray.size | 元素总个数 |
| ndarray.dtype | 每个元素类型 |
ndim = a.ndim print("当前数组维度数为:%d"%ndim) n,m = a.shape print("当前数组维度为%d*%d"%(n,m)) size = a.size print("当前数组元素总个数为%d"%(size)) dtype = a.dtype print("当前数组元素类型为%s"%(dtype))
当前数组维度数为:2 当前数组维度为2*3 当前数组元素总个数为6 当前数组元素类型为float64
import numpy as np np.random.rand(4)
array([0.07456414, 0.81147968, 0.03698034, 0.15820121])
2.1.1.4 ndarray切片
ndarray切片有一个非常重要的性质,就是可以根据维度来切片。
a = np.array([[1,2,3],[4,5,6]],dtype=float) print(a[0:1]) #按行切片,取第0行数据 print("-------------") print(a[:,1:3]) #按列切片,取第1列和第2列数据
[[1. 2. 3.]] ------------- [[2. 3.] [5. 6.]]
2.1.1.5 numpy广播
使用numpy最方便的地方之一就是一个直接对数组进行加法或乘法等运算。并且数组的运算法则遵循广播规则:
- 如果两个数组维度完全相同,则a*b结果即为各个位置元素相乘的结果,如下:
a=np.array([[1,2,3],[4,5,6]]) b=np.array([[1,2,3],[4,5,6]]) a*b
array([[ 1, 4, 9], [16, 25, 36]])
- 如果两个数组维度不同,则自动进行广播,例如常用的特征和权重相乘计算中:
X=np.array([[1,2,3],[4,5,6],[7,8,9]]) W=np.array([1,2,3]) X*W
array([[ 1, 4, 9], [ 4, 10, 18], [ 7, 16, 27]])
2.1.1.5 ndarray修改形状
import numpy as np a=np.arange(8) print("原始数组:",a) a=a.reshape(2,4) print("重组后的数组:",a)
原始数组: [0 1 2 3 4 5 6 7] 重组后的数组: [[0 1 2 3] [4 5 6 7]]
2.1.1.6 ndarray翻转(转置)数组
import numpy as np a = np.arange(15).reshape(3,5) print ('原数组:') print (a ) print ('\n') print ('转置后的数组:') print (np.transpose(a)) print ('\n') #也可以直接使用.T print ('转置后的数组:') print (a.T)
原数组: [[ 0 1 2 3 4] [ 5 6 7 8 9] [10 11 12 13 14]] 转置后的数组: [[ 0 5 10] [ 1 6 11] [ 2 7 12] [ 3 8 13] [ 4 9 14]] 转置后的数组: [[ 0 5 10] [ 1 6 11] [ 2 7 12] [ 3 8 13] [ 4 9 14]]
2.1.2 Numpy常用数学函数
import numpy as np a = np.arange(180) aSin=np.sin(a*np.pi/180)#sin aCos=np.cos(a*np.pi/180)#cos aTan=np.tan(a*np.pi/180)#tan print(np.exp(np.e))#e的n次幂 print(np.log(np.e))#ln函数
15.154262241479262 1.0
2.1.3 常用统计函数
统计数组中最大值,最小值等功能在对数值进行归一化时经常使用。
#numpy.amin(数组,axis=0/1) 用于计算数组中的元素沿指定轴的最小值。axis=0按列,axis=1按行 #numpy.amax(数组,axis=0/1) 用于计算数组中的元素沿指定轴的最大值 #numpy.ptp(数组,axis=0/1) 计算最大值和最小值的差 import numpy as np a=np.arange(10) a=a.reshape(5,2) print("原数组为:") print(a) print("\n") print("按列取最小值") print(np.amin(a,0)) print("\n") print("按行取最小值") print(np.amin(a,1)) print("\n") print("按列取最大值") print(np.amax(a,0)) print("\n") print("按行取最大值") print(np.amax(a,1)) print("\n") print("最大值和最小值的差为") print(np.ptp(a,0)) print("\n") #例如,如果要对a数值归一化,则可计算为 print("a数组归一化结果为:") amin=np.amin(a,0) aptp=np.ptp(a,0) print((a-amin)/aptp)
原数组为: [[0 1] [2 3] [4 5] [6 7] [8 9]] 按列取最小值 [0 1] 按行取最小值 [0 2 4 6 8] 按列取最大值 [8 9] 按行取最大值 [1 3 5 7 9] 最大值和最小值的差为 [8 8] a数组归一化结果为: [[0. 0. ] [0.25 0.25] [0.5 0.5 ] [0.75 0.75] [1. 1. ]]
2.1.4 排序函数
排序函数很多,从后面的学习来看比较有用的是numpy.argsort()。该函数,返回的是数组值从小到大的索引值。比如在KNN算法中,算完距离就需要排序得到前N的距离对应那些点,就可以用这个函数。例如:
import numpy as np res=np.array([4,2,3,6]) print(np.argsort(res))
[1 2 0 3]
2.1.5 Numpy矩阵Matrix
Numpy之前的ndarray可以产生的数组集合,看起来很像矩阵,但是从他的乘法运算我们可以明显看出来,他并不是真正的矩阵。Numpy矩阵运算可以调用他的线性代数函数库,个人感觉这个矩阵和数组混用太容易出问题了,因此我发誓以后绝不用矩阵,全部用数组,需要进行线性代数运算的全部调用线性代数函数。
import numpy as np A=np.mat([[1,2],[3,4]]) B=np.mat([[1,2],[3,4]]) C=A*B print("矩阵相乘的结果:") print(C) print("\n") D=np.array([[1,2],[3,4]]) E=np.array([[1,2],[3,4]]) print("数组相乘的结果:") F=D*E print(F)
矩阵相乘的结果: [[ 7 10] [15 22]] 数组相乘的结果: [[ 1 4] [ 9 16]]
2.1.6 Numpy线性代数运算函数
2.1.6 点积
数组的普通乘法直接用就行,如果要当矩阵计算,就直接调用dot函数
import numpy as np A=np.array([[1,2],[3,4]]) B=np.array([[1,2],[3,4]]) print("A=") print(A) print("\n") print("B=") print(B) print("\n") print("AB=") print(np.dot(A,B))
A= [[1 2] [3 4]] B= [[1 2] [3 4]] AB= [[ 7 10] [15 22]]
2.1.6 求逆矩阵
X = np.array([[1,2],[3,4]]) Y = np.linalg.inv(X) print("X=") print(X) print("\n") print("Y=") print(Y) print("\n") print("X dot Y =") print(np.dot(X,Y))
X= [[1 2] [3 4]] Y= [[-2. 1. ] [ 1.5 -0.5]] X dot Y = [[1.0000000e+00 0.0000000e+00] [8.8817842e-16 1.0000000e+00]]
2.2 Matplotlib(绘图库)
Matplotlib是一个 Python的绘图库,它以各种硬拷贝格式和跨平台的交互式环境生成出版质量级别的图形。
这个库感觉用来用去就那么几个常用的,记录一些比较重要的。
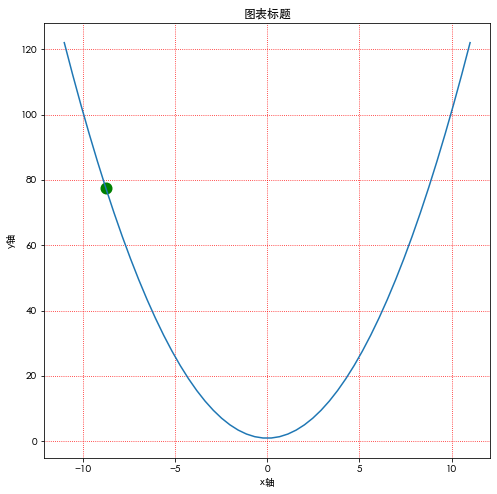
import numpy as np from matplotlib import pyplot as plt #x = np.arange(1,10) 生成离散的变量x x = np.linspace(-11, 11) y = x**2+1 #设置因变量 plt.rcParams['font.family']=['Heiti TC'] #选一个系统自带的中文字体,否则标题等地方无法现实中文 plt.figure(figsize=(8, 8)) #设置画布大小 plt.grid(ls=":",color='red',) #打开坐标网格 plt.title("图表标题") #设置标题 plt.xlabel("x轴") #设置x轴标题 plt.ylabel("y轴") #设置y轴标题 plt.plot(x[5], y[5], 'o', color='green', markeredgewidth=2, markersize=10) #画点 plt.plot(x,y) #画线 #plt.show()
[<matplotlib.lines.Line2D at 0x11e418f28>]
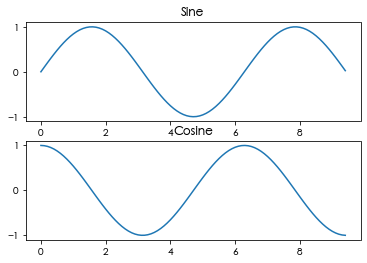
#还可以在一个画布里分两个子画布 import numpy as np import matplotlib.pyplot as plt x = np.arange(0, 3 * np.pi, 0.1) y_sin = np.sin(x) y_cos = np.cos(x) # 建立 subplot 网格,高为 2,宽为 1 # 激活第一个 subplot plt.subplot(2, 1, 1) # 绘制第一个图像 plt.plot(x, y_sin) plt.title('Sine') # 将第二个 subplot 激活,并绘制第二个图像 plt.subplot(2, 1, 2) plt.plot(x, y_cos) plt.title('Cosine') # 展示图像 plt.show()
- https://www.jianshu.com/p/da385a35f68d 这里还有各种柱状图、极坐标等画法、目前用不太到先存着