1.K近邻算法原理简介
KNN(k-Nearest Neighbors)也就是传说中的K近邻算法。这个算法的核心是如果一个样本和k个样本最相似,并且这k个样本大多数属于同一个分类,则这个样本也属于该分类。距离一般使用的是欧式距离,欧式距离的计算公式如下:
k近邻算法的基本流程就是以下几步:
- 1.计算输入点到所有样本点的欧式距离
- 2.欧式距离排序取最近的K个(通常是不大于20的整数)
- 3.找欧式距离最近的K个中所属分类最多的分类是哪个
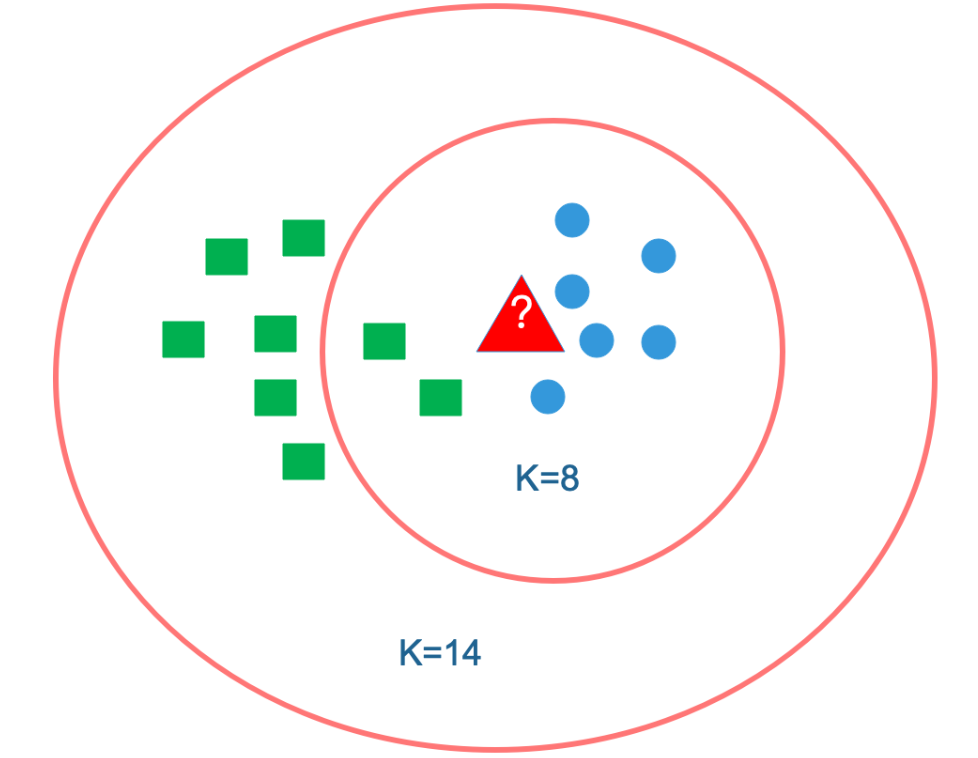
因此,从上面的计算过程我们可以发现,最重要的其实就是K值的选取。如果K值选的太大,考虑极限情况K=N,无论输入什么,都将被预测属于样本集中最多的类。如果K值选的太小,可能会发生过拟合。
2.K近邻算法使用案例
2.1 电影分类问题
这里使用根据电影中接吻镜头、打斗镜头等方法来判断电影类型作为案例。假设用于预测的样本数据集格式如下:
| 电影名称 | 打斗镜头数量 | 接吻镜头数量 |
|---|---|---|
| 使命召唤 | 100 | 0 |
| 功夫熊猫 | 115 | 0 |
| 极速追杀 | 135 | 0 |
| 101次求婚 | 0 | 5 |
| 爱的抱抱 | 1 | 13 |
| 基因决定我爱你 | 1 | 9 |
#创建数据集 import numpy as np import matplotlib.pyplot as plt def createDataSet(): group = np.array([ [0,5],[115,0],[135,0],[1,13],[1,9],[100,0]]) labels = ['B','A','A','B','B','A'] return group,labels
#数据集特征分布示意图 group,labels = createDataSet() plt.plot(group[:,0], group[:,1], 'o', color='green', markeredgewidth=2, markersize=10)
[<matplotlib.lines.Line2D at 0x1157b7e48>]

#假设新增一个影片,其中特征为70个打斗镜头和1个接吻镜头。 new_movie=[60,9] def takeElemNeedTobeSorted(elem): return elem[0] def classify(point,group,labels): dist_list = [] num = 0 for tmp_point in group: ##dist = np.sqrt((tmp_point[0]-point[0])**2+(tmp_point[1]-point[1])**2) #计算欧式距离 numOfFeature = len(tmp_point) #获取特征数量 dist=0 for i in range(numOfFeature): dist+=(tmp_point[i]-point[i])**2 #累加特征数量平方差 dist = np.sqrt(dist) dist_list.append([dist,num]) #保存距离和序号 num+=1 dist_list.sort(key=takeElemNeedTobeSorted) #按照距离排序 #统计前K个距离最近的点的类型,这里假设K是3 K=3 nearKTypeDict = {} for i in range(K): num = dist_list[i][1] if labels[num] in nearKTypeDict.keys(): nearKTypeDict[labels[num]]+=1 else: nearKTypeDict[labels[num]]=1 nearKTypeDict= sorted(nearKTypeDict.items(),key=lambda x:x[1],reverse=True)#根据类别数量排序 return nearKTypeDict[0][0] print("当前类别为%s"%classify(new_movie,group,labels))
当前类别为A
2.2 基于K近邻算法的约会网站配对优化
提供的样本特征主要包括一下三点: - 每年的飞行里程数 - 玩游戏看视频所占用时间的百分比 - 每周吃冰淇淋的公升数
样本集的分类有以下三种: - didntLike:不喜欢 - smallDoses:有点喜欢 - largeDoses:非常喜欢
数据文件名为:datingTestSet.txt,该文件为一千行文本文件,样例如下:
40920 8.326976 0.953952 largeDoses 14488 7.153469 1.673904 smallDoses 26052 1.441871 0.805124 didntLike
#读入数据,处理成符合之前分类函数的格式 import numpy as np def getDatingTestSet(): with open("attach/datingTestSet.txt") as f: data=f.read().split("\n") DatingTestSet = [] TestDatalabelSet = [] for i in data: data = i.split("\t") #print(data) if(len(data)>1): data[0] = float(data[0]) data[1] = float(data[1]) data[2] = float(data[2]) TestDatalabelSet.append(data[3]) data.pop() DatingTestSet.append(data) DatingTestSet = np.array(DatingTestSet) return DatingTestSet,TestDatalabelSet DatingTestSet,TestDatalabelSet = getDatingTestSet()
#对数值进行归一化处理:这里第一个特征的值明显大于其他两个,所以需要进行归一化处理 def dataNormal(dataSet): numOfFeature = len(dataSet[0]) for i in range(numOfFeature): minData = np.min(dataSet[:,i]) maxData = np.max(dataSet[:,i]) for data in dataSet: data[i] = (data[i]-minData)/(maxData-minData) return dataSet DatingTestSet = dataNormal(DatingTestSet) #print(DatingTestSet)
#将数据集划分成900个训练数据,100个测试数据。并进行测试 trainDataSet = DatingTestSet[0:900] testDataSet = DatingTestSet[900:1000] testDataLabel = TestDatalabelSet[900:1000] num = 0 trueNum = 0.0 falseNum = 0.0 for data in testDataSet: res = classify(data,trainDataSet,TestDatalabelSet) if res==testDataLabel[num]: trueNum +=1 else: falseNum +=1 num+=1 accuracy = trueNum/(falseNum+trueNum) errorRate = falseNum/(falseNum+trueNum) print("预测成功率为:%f\n"%accuracy) print("预测失败率为:%f\n"%errorRate)
预测成功率为:0.940000 预测失败率为:0.060000
参考链接:
- https://www.cnblogs.com/zhangkanghui/p/11289260.html 从0开始手工实现KNN
- https://blog.csdn.net/sinat_30353259/article/details/80901746 图和数学推导
- 《机器学习实战》