1 Decision Tree决策树算法
1.1 什么是决策树?
要想在全国近七亿女性中筛选出自己心仪的结婚对象是一件非常困难的事情,因此,我们需要设定一个标准。我们可以根据标准来选定该对象是否符合要求,例如:是否月入百万、是否有房有车、是否肤白貌美。根据上述条件我们可以建立出一颗如下图所示的决策树:
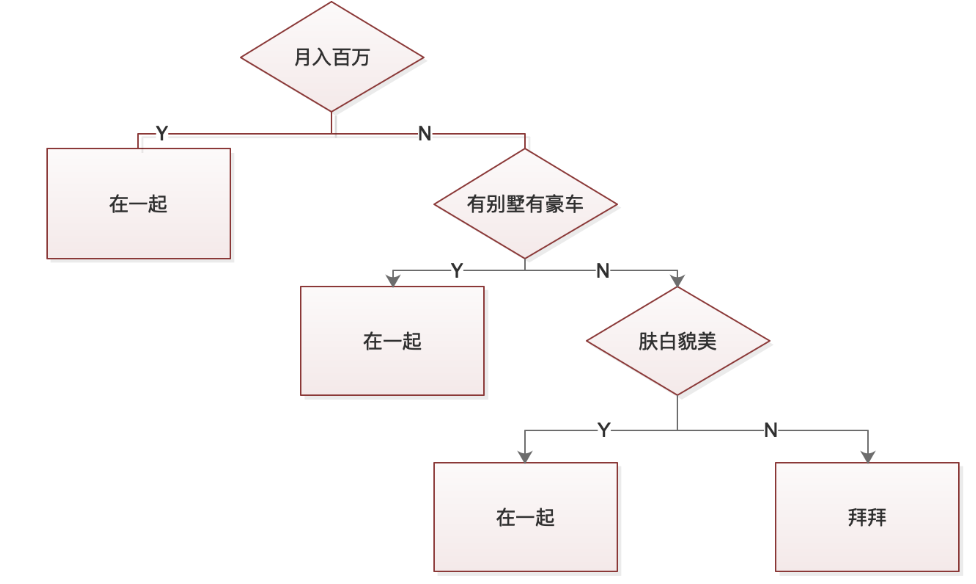
如上图所示,决策树的叶子结点代表决策结果,非叶子结点代表决策条件。从这里我们可以看出来,事实上一颗决策树建立的好坏与否,主要取决于特征的选取和阀值的选取。节点的选取比如上图中,我选取的第一个特征条件就是月收入情况,而阀值为100万。如果节点和阀值的选取合理,则可以选择出心仪的对象。
1.2 节点选取的衡量指标
对数据划分的基本原则,应该将无序的数据变得更加有序。在划分数据集前后信息发生的变化称为信息增益,获得信息增益最高的特征就是最好的选择。
1.2.1 信息熵
什么是信息熵呢?熵原本是物理学中用于度量一个热力系统的混乱程度的属性。信息学中的熵,代表一条信息所可能蕴含信息量的大小。熵越大也就代表着可能蕴含的信息量越大。信息熵的计算公式如下:
一个系统越复杂,越无序,所蕴含的信息量越大,这个值就越大。
1.2.2 GINI(基尼)系数
基尼系数也是用来衡量信息的复杂度的一个值。当类别越少,类别集中度越高的时候,基尼系数越低;当类别越多,类别集中度越低的时候,基尼系数越高。 在分类问题中,假设存在K个分类,样本点属于低k个分类的概率为则基尼系数的计算公式如下:
对于给定样本集D,若存在K个分类,则其基尼系数可以计算如下:
对于样本D,个数为|D|,根据特征A的某个值a,把D分成D1和D两个子集,则在特征A的条件下,样本D的基尼系数表达式为:
1.2.3 条件熵和信息增益
条件熵H(Y|X)表示在已知随机变量X的情况下,随机变量Y的不确定性。在X给定的条件下,H(Y|X)可计算如下:
在计算出上述条件熵的基础上,我们可以进行信息增益的计算。设特征A对训练数据集D的信息增益为,则信息增益计算如下:
事实上信息增益的大小是相对于训练数据集而言的,并无绝对意义。也就是说,即便信息增益很大,但如果源数据熵很大,也不能说明这个分类带来的收益就很大。因此,为了解决这个问题,引入了信息增益比,信息增益比的计算方法如下:
1.2.4 例题 计算经验熵、增益比
例:计算信息增益计算例题,以个人条件和申请贷款成功与否作为统计数据进行信息增益比计算。数据如下图所示:
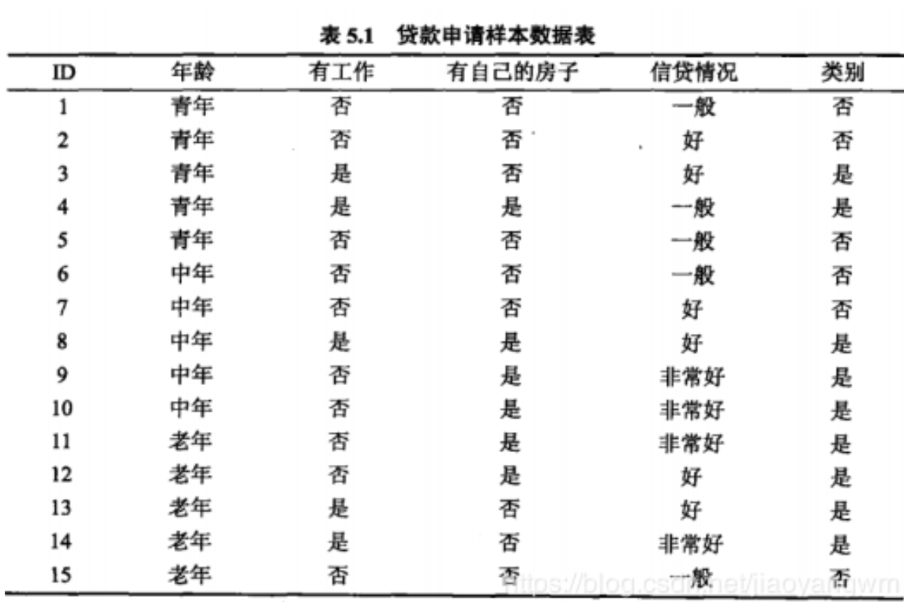
def creatDataSet(): #定义一下数据集 dataSet=[[0, 0, 0, 0, 'no'], [0, 0, 0, 1, 'no'], [0, 1, 0, 1, 'yes'], [0, 1, 1, 0, 'yes'], [0, 0, 0, 0, 'no'], [1, 0, 0, 0, 'no'], [1, 0, 0, 1, 'no'], [1, 1, 1, 1, 'yes'], [1, 0, 1, 2, 'yes'], [1, 0, 1, 2, 'yes'], [2, 0, 1, 2, 'yes'], [2, 0, 1, 1, 'yes'], [2, 1, 0, 1, 'yes'], [2, 1, 0, 2, 'yes'], [2, 0, 0, 0, 'no']] labels=['年龄','有无工作','有无自己的房子','信贷情况'] return dataSet,labels
#计算经验熵 from math import log def calculatingEmpiricalEntropy(dataSet): dataCount = len(dataSet) resLabelCount = {} for people in dataSet: #获取结果有几个yes几个no currentResLabel = people[-1] if currentResLabel not in resLabelCount.keys(): resLabelCount[currentResLabel] = 0 resLabelCount[currentResLabel]+=1 empiricalEntropy=0.0 for key in resLabelCount: Pi = float(resLabelCount[key]/dataCount) empiricalEntropy += -(Pi)*log(Pi,2) #根据公式计算经验熵 #print("当前数据集经验熵为:"+str(empiricalEntropy)) return empiricalEntropy dataSet,labels=creatDataSet() calculatingEmpiricalEntropy(dataSet)
0.9709505944546686
#计算各个标签的信息增益 def splitDataSet(dataSet,axis,value): retDataSet=[] for featVec in dataSet: if featVec[axis]==value: reducedFeatVec=featVec[:axis] reducedFeatVec.extend(featVec[axis+1:]) retDataSet.append(reducedFeatVec) return retDataSet def CalcGainRatio(dataset): numOfFeatures = len(dataSet[0]) - 1 baseEntropy = calculatingEmpiricalEntropy(dataSet) print(baseEntropy) for i in range(numOfFeatures): featList = [example[i] for example in dataSet] uniqueVals = set(featList) newEntropy = 0.0 for value in uniqueVals: #subDataSet划分后的子集 subDataSet = splitDataSet(dataSet, i, value) #计算子集的概率 prob = len(subDataSet) / float(len(dataSet)) #根据公式计算经验条件熵 newEntropy += prob * calculatingEmpiricalEntropy((subDataSet)) infoGain = baseEntropy - newEntropy #打印每个特征的信息增益 print("第%d个特征的增益为%.3f" % (i, infoGain)) dataSet,labels = creatDataSet() CalcGainRatio(dataSet)
0.9709505944546686 第0个特征的增益为0.083 第1个特征的增益为0.324 第2个特征的增益为0.420 第3个特征的增益为0.363
1.3 ID3算法、C4.5算法、CART算法算法核心简述
- ID3算法(递归找最大的信息增益特征):其实上面计算的过程就是ID3算法的核心过程,对每一使用个特征计算信息增益,然后挑一个信息增益最大的作为当前子集划分的特征。然后把里面结果为满足当前选中特征的那部分作为集合1,剩下那一部分作为集合2,然后对于集合2再次递归的进行这种操作。知道所有的特征均用完或者信息增益都特别小。
- C4.5算法(递归找最大的信息增益比特征):就是把选取特征的标准从信息增益最大,改成了信息增益比最大。极端情况下,如果每个特征都只有一个元素,那么使用ID3算法计算的信息增益就是0,使用C4.5算法,可以减少因特征值多导致信息增益大的问题。
- CART算法(递归找基尼系数最小的特征):计算每个特征的基尼系数,取基尼系数最小的点作为特征。G(D,A)计算公式如下: 对于样本D,个数为|D|,根据特征A的某个值a,把D分成D1和D两个子集,则在特征A的条件下,样本D的基尼系数表达式为:
参考:
- https://blog.csdn.net/jiaoyangwm/article/details/79525237 ID3算法
- https://blog.csdn.net/fuqiuai/article/details/79456971 C4.5算法
- https://www.cnblogs.com/keye/p/10564914.html CART算法