1. SVM支持向量机

1.1 SVM基本原理

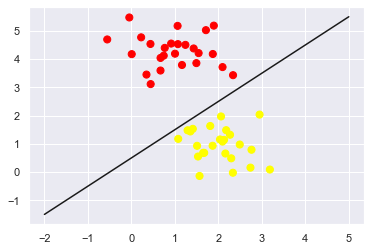
SVM(Support Vector Machine)中文名为支持向量机，在机器学习领域属于常见的有监督学习。一如下图所示的两堆点为例子，黄色和黑色的点显然是两种不同的类别，如果想将他们区分开来。可以通过画一条直线，作为两堆点的分界线。

import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
import numpy as np
X, y = make_blobs(n_samples=50, centers=2,
                  random_state=0, cluster_std=0.60)#随机生成两组点
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
xfit = np.linspace(-2, 5)
plt.plot(xfit, 1 * xfit + 0.5, '-k')

[<matplotlib.lines.Line2D at 0x1246dfc18>]

当纬度升高时，超平面的公式可以概括为 $$W^{T}X+B=0$$ $$其中X为特征向量$$

总的来说，支持向量机算法中，最核心的部分就是要求出$W^{T}$和$B$，因此训练过程就是要想办法求出最优的$W^{T}$和$B$。而预测过程就是对输入数据提取特征向量$X$，然后带入方程计算，得出当前点在超平面分割后空间中哪个区域，得出预测结果。可以看得出，其实在训练数据中，有一部分点对于超平面选取的影响至关重要，如上图，离直线最近的红点和黄点，这些对于分离超平面影响较大的数据点也被称为支持量。而最优的超平面显然就是一个到各个支持向量距离相等，并且这个距离最大的平面，根据公式，因为距离相等所以他们的$W^{T}X+B$也相等。

事实上，求解$W_T$和$B$的过程也就是要让分类中里超平面最近的这些点，和超平面间的距离尽可能的大。

如何求间距最大的超平面呢？

设：

• 超平面为：$W^TX+B=0$
• 分类函数为：$classify(X) = sign(W^T+B)$（sign函数表示输入大于0为1，小于0为-1，等于0为0）
• 支持向量到超平面距离为：$d(X)=\frac{W^TX+B}{\left | W^T \right |}$,${\left | W^T \right |}$表示W的二范式。也就是所有元素的平方求和，再开方。

现在的目的就是要让特征点处$d(X)=\frac{W^TX+B}{\left | W^T \right |}$最小。由于各个特征点到分离面距离相同，所以$W^TX+B$在各个特征点的值也相同等于某个定值，干脆就假设$W^TX+B=1$。这样问题转化成了求:

$$max(\frac{1}{\left | W^T \right |})$$

这个函数的最大值点，等同于下面这个函数的最小值点 $$min(\frac{1}{2}{\left | W^T \right |}^2)$$

当然，还有一个限制条件，之前我们假设了标签分类结果为1或者-1。支持向量处$W^TX+B=1或-1$。正确预测的情况下， $$label*(W^TX+B)=1\\ 其中label为分类标签1或-1$$

最后问题转换成了求： $$min(\frac{1}{2}{\left | W^T \right |}^2)$$ 限制条件为： $$label*(W^TX+B)=1$$

后面的推导还用了拉格朗日乘子法,然后神奇的推导成了使用拉格朗日乘子法求: $$max(\sum_{i=1}^{m}\alpha_i-\frac{1}{2}\sum_{i,j=1}^{m}label_i*lable_j*\alpha_i*\alpha_j*<x_i,x_j>)\\ 尖括弧表示内积，约束条件为：\\ \sum_{i=1}^{m}\alpha_i*label_i=0$$

1.2 核函数

假如在原始的特征纬度中无法找到一个能够分割数据的超平面，那么就需要核函数的帮助。所谓的核函数，本质上是将原始特征映射到一个高纬度空间，从而解决原始空间无法线性分割的问题。以下图为例，在下图的这个一纬度空间中，我们如无法找到一个分界点，将绿色点和黄色点正确分开。

import matplotlib.pyplot as plt
plt.plot([-0.1,-0.2,-0.3], [0,0,0], 'o', color='yellow', markeredgewidth=2, markersize=10)
plt.plot([0.2,0.4,0.6], [0,0,0], 'o', color='green', markeredgewidth=2, markersize=10)
plt.plot([1.1,1.2,1.3], [0,0,0], 'o', color='yellow', markeredgewidth=2, markersize=10)

[<matplotlib.lines.Line2D at 0x125a31978>]

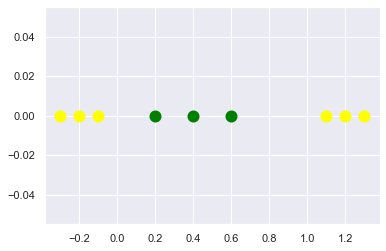
为了解决上述问题，我们可以把该一纬特征映射到更高纬度的二维空间$x^2和x$中，如下图所示：

import matplotlib.pyplot as plt
plt.figure(figsize=(8, 8))#设置画布大小
ax = plt.gca()
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))

plt.plot([-0.1,-0.2,-0.3], [0.01,0.04,0.09], 'o', color='yellow', markeredgewidth=2, markersize=10)
plt.plot([0.2,0.4,0.6], [0.04,0.16,0.36], 'o', color='green', markeredgewidth=2, markersize=10)
plt.plot([1.1,1.2,1.3], [1.21,1.44,1.69], 'o', color='yellow', markeredgewidth=2, markersize=10)
xfit = np.linspace(-0.5, 1.5)
plt.plot(xfit, 1 * xfit, '-k')

[<matplotlib.lines.Line2D at 0x126474400>]

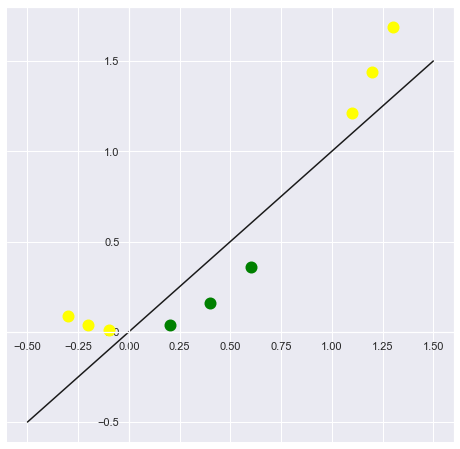
此时，我们可以构建分离超平面$x^{2}-x=0$将原本线性不可分的问题解决。

参考链接：

• https://www.cnblogs.com/shayue/p/10399143.html 画图的
• https://blog.csdn.net/fuqiuai/article/details/79483057 svm算法原理讲解
• https://www.jianshu.com/p/f7d2ed8aac54 svm算法代码实现
• https://blog.csdn.net/qq_35992440/article/details/80987664 svm数学推导