1.6 Neural Network 神经网络

神经网络的基本概念前面已经学习过了，现在比较流行的就是深度神经网络。也就是隐藏层特别多的神经网络。神经网络有许多的神经元组成，该算法的灵感来源于人体的神经元细胞。神经元细胞接收刺激，当刺激达到一定程度的时候就会被激发，产出神经递质。基于上述特征，算法设计类似神经网络的图，各个节点接收上一层所传来的“刺激值”（特征值），根据不同的权重对特征值求加权和，判断加权和和阀值的大小，然后使用阶跃函数判断输出。神经网络中节点工作示意图如下：

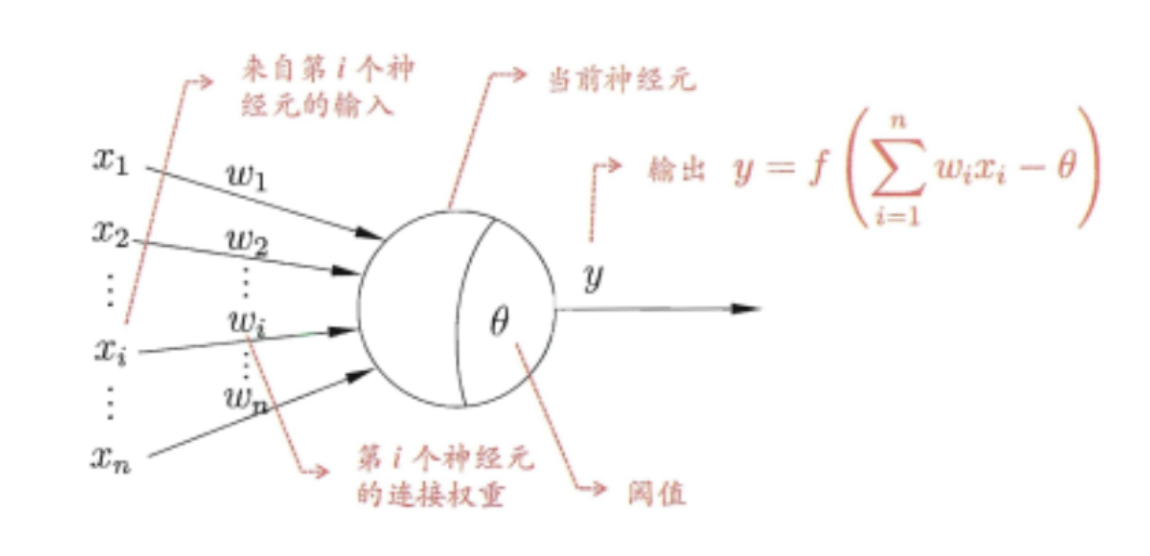
因此，所谓的训练过程，其实就是要想办法求出各个边的权重$w_i$和各个神经元的阀值。常用的激活函数一般有：

• sigmoid函数：S型生长曲线，$f(x)=\frac{1}{1+e^{-x}}$
• ReLU（Rectified Linear Unit）函数：线性整流函数，$f(x)=max(0,x)$

在神经网络中，训练调整权重和阀值时，最重要算法就是误差逆传播算法（error BackPropagation），简称BP算法，其实简单来说就是一个链式求导法则。以下以下图所示的一个神经网络作为例子：

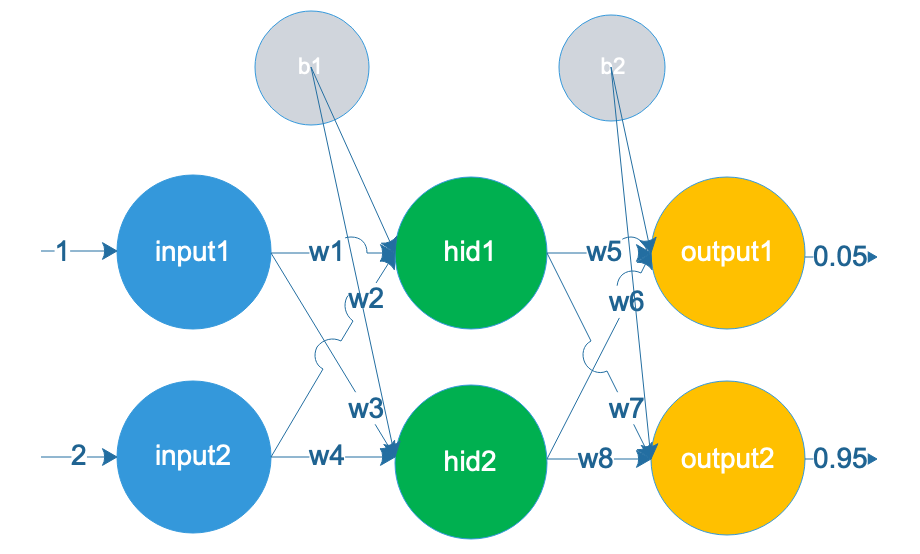
假设上图中的神经网络中，读入为输入数据为：$i_1=1,i_2=2$，要求输出数据为：$o_1=0.05,o_2=0.95$

假设现在只使用了这一组训练数据$x_1=[1,2]$进行训练。首先在[0,1]直接随机生成一组权重$w_i$,和$b_i$，为了方便这里b每层公用一个。

1.生成随机权重

import numpy as np
w_list = np.random.random(8) #随机生成8个初始权重
b_1= np.random.random(1)[0]
b_2= np.random.random(1)[0]
num=1
for i in w_list:
    print("第%d个特征值：w%d=%f"%(num,num,i))
    num+=1
print("阀值b1：b1=%f"%b_1)
print("阀值b2：b2=%f"%b_2)

第1个特征值：w1=0.271979
第2个特征值：w2=0.061594
第3个特征值：w3=0.096432
第4个特征值：w4=0.975282
第5个特征值：w5=0.660006
第6个特征值：w6=0.003519
第7个特征值：w7=0.858528
第8个特征值：w8=0.974995
阀值b1：b1=0.901945
阀值b2：b2=0.101353

2.计算当前输出的$o_1$和$o_2$，

这里我们激活函数使用sigmod函数： $$\begin{array}{l} hid{1_{out}} = f({x_1}{w_1} + {x_2}{w_2} - {b_1}) = \frac{1}{{1 + {e^{ - ({x_1}{w_1} + {x_2}{w_2} - b)}}}}\\ hid{2_{out}} = f({x_1}{w_3} + {x_2}{w_4} - {b_1}) = \frac{1}{{1 + {e^{ - ({x_1}{w_3} + {x_2}{w_4} - b)}}}}\\ output{1_{out}} = f(hid{1_{out}}{w_5} + hid{2_{out}}{w_6} - {b_2}) = \frac{1}{{1 + {e^{ - (hid{1_{out}}{w_5} + hid{2_{out}}{w_6} - {b_2})}}}}\\ output{2_{out}} = f(hid{1_{out}}{w_7} + hid{2_{out}}{w_8} - {b_2}) = \frac{1}{{1 + {e^{ - (hid{1_{out}}{w_7} + hid{2_{out}}{w_8} - {b_2})}}}} \end{array}$$

hid1_out=1/(1+np.e**-(1*w_list[0]+2*w_list[1]-b_1))
hid2_out=1/(1+np.e**-(1*w_list[2]+2*w_list[3]-b_1))
output1_out=1/(1+np.e**-(hid1_out*w_list[4]+hid2_out*w_list[5]-b_2))
output2_out=1/(1+np.e**-(hid1_out*w_list[6]+hid2_out*w_list[7]-b_2))
print("hid1_out：%f"%hid1_out)
print("hid2_out：%f"%hid2_out)
print("output1_out：%f"%output1_out)
print("output2_out：%f"%output2_out)

hid1_out：0.375949
hid2_out：0.758606
output1_out：0.537292
output2_out：0.723331

3.计算反向传播误差

首先计算误差，这里我们使用均方误差（MSE）来定义损失，也就是损失函数,计算公式如下。 $$E = \frac{1}{n}{\sum\limits_{i = 1}^n {({y_{real}} - {y_{pred}})} ^2}$$

MSE = 1/2*((output1_out-0.05)**2+(output2_out-0.95)**2)
print("总误差为：%f"%MSE)

总误差为：0.144416

3.含隐曾权值更新

假设我们想要知道$w_8$对于整体的误差有多大影响，我们可以使用链式求导法则对$w_8$求偏导数。这也是BP算法的核心内容。求导公式为： $$\frac{{\partial E}}{{\partial {w_8}}} = \frac{{\partial E}}{{\partial output{2_{out}}}} \cdot \frac{{\partial output{2_{out}}}}{{\partial {w_8}}} = \frac{{\partial E}}{{\partial output{2_{out}}}} \cdot \frac{{\partial output{2_{out}}}}{{\partial {w_8}}}$$

因此这里就是要分别求出$\frac{{\partial E}}{{\partial output{2_{out}}}} 和 \frac{{\partial output{2_{out}}}}{{\partial {w_8}}}$

$$\begin{array}{l} E = \frac{1}{2}{(0.05 - output{1_{out}})^2} + \frac{1}{2}{(0.95 - output{2_{out}})^2}\\ \frac{{\partial E}}{{\partial output{2_{out}}}} = 0 + 2 \times \frac{1}{2} \times (0.95 - output{2_{out}}) - 1 = 0.9 - output{2_{out}} \end{array}$$

delEToOutput2=0.9-output2_out
print("均方误差MSE关于output2_out的偏导数为：%f"%delEToOutput2)

均方误差MSE关于output2_out的偏导数为：0.176669

$$\begin{array}{l} output{2_{out}} = \frac{1}{{1 + {e^{ - (hid{1_{out}}{w_7} + hid{2_{out}}{w_8} - {b_2})}}}}\\ \frac{{\partial output{2_{out}}}}{{{w_8}}} = output{2_{out}}*(1 - output{2_{out}})*hid{2_{out}} \end{array}$$

delOutput2ToW8=output2_out*(1-output2_out)*hid2_out
print("输出层第二个节点的输出关于w8的偏导数为：%f"%delOutput2ToW8)

输出层第二个节点的输出关于w8的偏导数为：0.151815

#将以上两个偏导数相乘即可得到E关于w8的偏导数
delEtoW8=delEToOutput2*delOutput2ToW8
print("E关于w8的偏导数为：%f"%delEtoW8)

E关于w8的偏导数为：0.026821

此时我们就可以来更新$w_8$的值，当然，我们需要选一个更新的步长，比如我这里选择$\eta=0.66$。那么更新公式为 $$w_8^新=w_8-\eta*\frac{{\partial E}}{{\partial {w_8}}}$$

w_8=w_list[7]-0.66*delEtoW8
print("更新前的w8为：%f",w_list[7])
print("更新后的w8为：%f",w_8)

更新前的w8为：%f 0.9749950376883143
更新后的w8为：%f 0.9572932735464927

之后依次计算各个点的权值更新，然后使用新的权值再次计算输出，循环往复，直到误差值小于规定要求。

参考：

• https://www.cnblogs.com/maybe2030/p/5597716.html [Deep Learning] 神经网络基础
• https://www.jianshu.com/p/53445edf8199 神经网络Neural Network
• https://blog.csdn.net/zhaomengszu/article/details/77834845 大白话讲解BP算法
• https://www.cnblogs.com/maybe2030/p/5597716.html [Deep Learning] 神经网络基础,大佬笔记