1.K-Means聚类算法
1.1 K-Means聚类算法基本原理
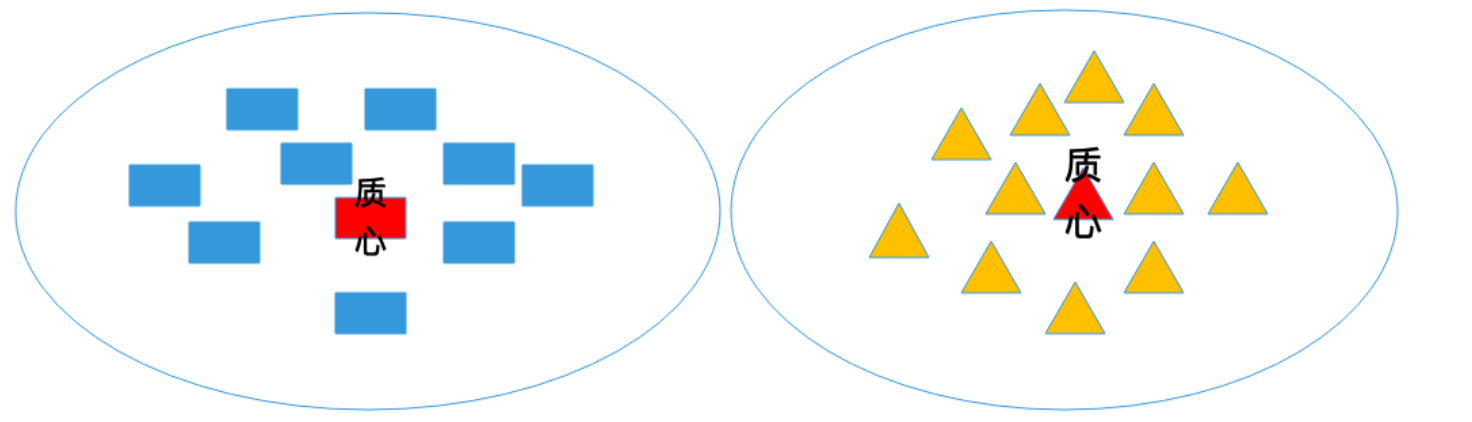
聚类就是将一大堆数据集中,将具有相同特征的数据自动的归到一类,每一类都称为一个簇。很显然这是一种无监督学习方法。所谓的K-Means(K-均值)算法就是用来发现数据集中K个簇的算法,并且每个簇的中心使用簇中的均值来确定,每个簇的中心叫做质心。
这里的距离一般采用欧式距离来进行计算: 两者欧式距离计算公式为:
1.2 K-Means聚类算法流程简述
算法流程简述:
- 1.随机创建K个点作为初始质心(不一定是数据集中的点)
- 2.分别计算每个数据和质心的欧式距离,并将该数据分类至距离最近的簇,如果簇发生变化则进行记录
- 3.对每一个簇,统计簇中所有的数据点特征的平均值作为新的质心
- 4.弱在上述步骤中不存在簇发生变化的情况发现则算法结束,否则跳转至第2步
1.3 K-Means聚类算法评价标准
K-Means聚类算法一般采用SSE (Sum of Squared Error, 误差平方和 )作为评价标准,也就是每一个点到其所在簇质心的距离的平方的总和。SSE值越小,表明簇内所有点越接近质心,分类效果越好。
1.4 K-Means聚类算法实例
给定的数据集是一个八十行的数据文件,每行两个特征值。现在要求根据这个特征值进行聚类,部分数据集如下:
1.658985 4.285136 -3.453687 3.424321 4.838138 -1.151539 -5.379713 -3.362104 0.972564 2.924086 -3.567919 1.531611 0.450614 -3.302219 -3.487105 -1.724432 2.668759 1.594842
首先从文件中,读入数据,将原始数据转换成np数组
import numpy as np #数据读入函数 def loadData(filename): with open(filename,"r") as f: fileContent = f.read() data = fileContent.split("\n") dataMat = [] for row in data: if row!="": item = row.split("\t") dataMat.append(item) dataMat = np.array(dataMat,dtype="float64") return dataMat dataSet = loadData("attach/1.8/testSet.txt")
各个数据特征分布如下图所示:
#特征分布图 from matplotlib import pyplot as plt for row in dataSet: plt.plot(row[0], row[1], 'o', color='green', markeredgewidth=2, markersize=10) #画点

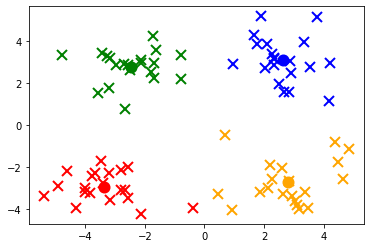
从图中,我们可以观察出给定数据整体可以分为四个簇,为方便后续计算我们先构建一个计算两个特征向量欧式距离的函数。
import numpy as np def distCalc(vecX,vecY): dist = np.sqrt(np.sum(np.power((vecX-vecY),2)))#神奇的数组计算大大降低了代码量 return dist #print(distCalc(dataSet[0],dataSet[1]))
完成准备工作开始,算法编写,根据算法的基本流程,第一步是要构建k个随机质心
import numpy as np def makeRandCent(dataSet,k): #随机质心创建的时候要注意,质心要在范围空间内 n = dataSet.shape[1] #获取特征数量 centList = np.zeros((k,n)) for i in range(n): minI = np.min(dataSet[:,i]) rangeI = np.max(dataSet[:,i])-minI centList[:,i] = minI + rangeI*np.random.rand(1,k) return centList centList = makeRandCent(dataSet,4) #生成随机的质心
print(centList)
[[ 0.65663247 0.77717004] [-0.84559261 -0.73683408] [-0.61538579 0.69684389] [ 0.70073271 -0.68287865]]
def kMeans(dataSet,k): typeChange = True numOfdata = dataSet.shape[0] dataClassifyRes = [-1]*80 while typeChange: typeChange = False indexOfData = 0 for data in dataSet: num=0 minDist = np.inf minIndex = -1 for cent in centList: dist = distCalc(data,cent) if dist<minDist: minDist = dist minIndex = num num+=1 if minIndex==dataClassifyRes[indexOfData]: pass else: dataClassifyRes[indexOfData]=minIndex #print(indexOfData,"------》",minIndex) typeChange = True indexOfData+=1 #更新k个质心的特征值 for i in range(k): indexListOfThisType = [] for index,value in enumerate(dataClassifyRes): if value==i: indexListOfThisType.append(index) for j in range(centList.shape[1]): SUM = 0.0 for index in indexListOfThisType: SUM += dataSet[index][j] centList[i][j] = (SUM/(len(indexListOfThisType))) return dataClassifyRes res = kMeans(dataSet,4)
from matplotlib import pyplot as plt for index,value in enumerate(res): if value==0: plt.plot(dataSet[index][0], dataSet[index][1], 'x', color='green', markeredgewidth=2, markersize=10) #画点 if value==1: plt.plot(dataSet[index][0], dataSet[index][1], 'x', color='red', markeredgewidth=2, markersize=10) #画点 if value==2: plt.plot(dataSet[index][0], dataSet[index][1], 'x', color='blue', markeredgewidth=2, markersize=10) #画点 if value==3: plt.plot(dataSet[index][0], dataSet[index][1], 'x', color='orange', markeredgewidth=2, markersize=10) #画点 #画出四个质心点 plt.plot(centList[0][0], centList[0][1], 'o', color='green', markeredgewidth=2, markersize=10) #画点 plt.plot(centList[1][0], centList[1][1], 'o', color='red', markeredgewidth=2, markersize=10) #画点 plt.plot(centList[2][0], centList[2][1], 'o', color='blue', markeredgewidth=2, markersize=10) #画点 plt.plot(centList[3][0], centList[3][1], 'o', color='orange', markeredgewidth=2, markersize=10) #画点
[<matplotlib.lines.Line2D at 0x119bc2e10>]